本文为摘录，原文为： attachments/pdf/7/p46-li.pdf

  • 查询重写使用启发式算法来实现，有两个限制

    • 规则的应用顺序严重影响查询性能，但
      • 可能的重写顺序随查询涉及到的算子指数增长
      • 受限于搜索空间大小限制，很难找到最佳的顺序
    • 针对不同的查询，不同的重写规则的收益也不同
      • 当前的方法，只能应用于单个计划，而不能有效的估计查询重写的收益

  • 提出了基于策略树树的查询重写框架

1 INTRODUCTION

  • 查询重写：将一个 SQL 查询转换成为等价的、但性能更高的 SQL.

  • 规则的应用顺序严重影响查询性能， 以 下图 为例：

    • q1

      • 采用传统的从上到下的顺序应用规则
      • 仅能应用 O1 和 O3
      • 执行时间 >20 min

    • q2

      • 通过策略树实现 O1,O4,O3,O5 的顺序应用规则
      • 执行时间 1.941s

      性能相差 600 倍。

  • 传统方法通过匹配预定义的规则顺序来重写
    • 可能会陷入局部最优解

2 LearnedRewrite

2.1 树形结构

  • 使用 策略树 表达可能的顺序：

    • 根节点 root: 表示输入的原始 SQL
    • 每个非根节：点表示对其父节点应用重新规则之后生成的新的查询
    • 根节点到其他节点的路径：表示重新的顺序

  • 策略树的优势

    • 不同路径，可以共享相同的祖先 （已经重写的查询）
      • 避免重复应用规则
    • 可以通过蒙特卡罗树搜索 (Monte Carlo Tree Search, MCTS) 来探索策略树从而找到优化节点

3 PRELIMINARIES

3.1 Query Rewrite Rules

3.1.1 Input Query

3.1.2 Query Tree

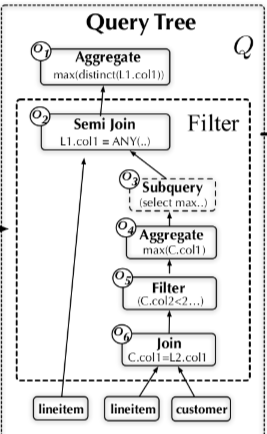
3.1.3 Query Rewrite Rules

  • 规则：针对查询的等价变换
  • 定义： \[r = (o,c,a)\]
    • 含义：
      • o: operator, 算子
      • c: condition, 条件
      • a: rewrite action
    • 解释：对于指定的查询 q ，规则
      • 首先匹配到算子 o
      • 如果 c 满足，或者 o 是子树的 root, 则对 q 应用 a ，得到 \[q^{(o,r)}\] ,
      • q 和 \[q^{(o,r)}\] 等价

3.1.4 Rewrite Benefit of Applying A Rewrite Rule

\[\Delta Cost(q^{(0,r)},q) = Cost(q) - Cost(q^{(o,r)})\] where:

  • \[Cost(q)\] : 重写之前的代价
  • \[Cost(q^{(o,r)})\] ： 重写之后的代价

3.1.5 The Rewrite Order of Applying Multiple Rewrite Rules

3.2 Query Rewrite

3.2.1 Query Rewrite

  • Human-involved methods

    • 手动干预
    • 性能高
    • 分析，决策耗时长

  • Heuristic query rewrite 启发式 （如 PG）

    • 自顶向下遍历查询计划中的算子，对每个算子：

      • 如果匹配到规则，则应用规则

    • 效率更高，但有两个主要限制：

      • 应用规则的顺序是固定的 可能会错过更好的重写顺序
      • 该方法不考虑重写的收益 可能会导致重写无用、甚至变得更慢

3.2.2 Learning Models for Databases

3.2.3 Reinforcement Learning

4 TREE SEARCH FOR QUERY REWRITE

4.1 Overview of Policy Tree Search

  • Policy Tree: Given a query q and a set of rewrite rules, we build a policy tree T , where the root node denotes the origin query q, any non-root node denotes a rewritten query (that transforms the query of its parent by applying a rewrite operation), and a leaf denotes a query that cannot be rewritten by any rewrite rules.