Chimp: Efficient Lossless Floating Point Compression for Time Series Databases

• 1 ABSTRACT
• 2 INTRODUCTION
• 3 PRELIMINARIES
  • 3.1 Floating Point Time Series
  • 3.2 IEEE 754 Double Precision Floating Point Format
  • 3.3 Gorilla Compression
• 4 PROPERTIES OF REAL-WORLD TIME SERIES
  • 4.1 Trailing Zeros
  • 4.2 Leading Zeros
  • 4.3 Revisiting Gorilla Compression
• 5 OVERVIEW
  • 5.1 Our Chimp Algorithm
• 6 效果对比
  • 6.1 Compression size result
  • 6.2 Compression and decompression time

本文为摘录，原文为： attachments/pdf/1/p3058-liakos.pdf

1 ABSTRACT

• 时序数据难以高效存储，导致存储代价高昂。

• 通用压缩 技术可以减少数据大小，但给计算带来额外开销。

  • 通常不能忍受

• 通常采用快速、 流式压缩 将数据进行编码

  • 该做法无法完全使用压缩的潜力

• Chimp

  • 新型流式压缩算法
  • 适用于时间序列的浮点数运算
  • 压缩比与通用算法相当，比目前标准的流式压缩比高 50%
  • 压缩、解压时间更短

2 INTRODUCTION

• TSMS: Time Series Management Systems
• TSMS 压缩存储浮点数据的方法：
  • 将当前值与前一时刻的值进行异或运算 （XOR）
  • 得到的值中，大概率很多的 bit 会是 0:
    • 因为数据一般不会突然变化很大
• 我们发现，相邻数据 XOR 的结果：
  • 0 通常不会出现在结果的尾部
  • 而是出现在头部

3 PRELIMINARIES

3.1 Floating Point Time Series

• 时间序列， Time series （TS）

  • 一系列的数据点
  • 数据点是一对 时间戳 和 值
  • 数据点按照时间递增排序
  • \[TS=\langle(\,t_1, v_1 )\,,(\,t_2, v_2 )\, ,… \rangle \]
    • \(t_i\) 表示时间戳
    • \(v_i\) 表示值

• Bounded Time series

  • 特殊的时间序列
  • 拥有固定个数的时间序列 \[TS=\langle(\,t_1, v_1 )\,,…,(\,t_n, v_n )\, \rangle \]

• Floating Point Time series

  • 特殊的时间序列
  • \[TS=\langle(\,t_1, v_1 )\,,(\,t_2, v_2 )\, ,… \rangle \] 满足：
    • \[v_i \in \mathbb{R}\]
    • \[i \in \mathbb{N}\]

3.2 IEEE 754 Double Precision Floating Point Format

• 双精度浮点数的格式
  • 符号位， Sign (S)
    • 1 bit
    • 0: 正
    • 1: 负
  • 指数位, biased exponent (E)
    • 11 bits
    • 偏移为 1023
  • 分数位, Fractional (F)
    • 52 bits
• 数学表示： \[x = (-1)^s \times 2 ^{(E-B)} \times 1.F\]

3.3 Gorilla Compression

• Gorilla 的变长编码：
  • 第一个数值不压缩
  • 后续数值与前一个做 XOR:
    • 结果为 0 （即两者相等）， 则存 0
    • 如果不为 0 ：则存 1 ， 后接：

      • 控制位 0 ： 当前有效位数在前者有效位数范围内，即：

        1. 当前值（XOR 后）的 leading zeros 的个数大于前值的 leading zeros, 且
        2. 当前值的 trailing zeros 的个数大于前值的 trailing zeros

        此情况下使用前值的信息，在控制位后进保存 XOR 后的有效数值

      • 控制位 1 ：

        • 使用接下来的 5 bits 来保存 leading zero 的个数
        • 使用接下来的 6 bits 来保存 XOR 结果的有效数值长度
        • 最后保存 XOR 结果的有效数值

4 PROPERTIES OF REAL-WORLD TIME SERIES

4.1 Trailing Zeros

4.2 Leading Zeros

4.3 Revisiting Gorilla Compression

4.3.1 Flag Bits.

前面介绍 Gorilla 的 flag bits 有三种： 0 ， 10 和 11 。其中 0 表示当前值和前面的值相等。 然而这种情形并不常见。

如果能够使用最少的比特位来表示最常见的情况，则应该能够提升压缩比。

4.3.2 Length of Meaningful XORed Value (Center Bits).

4.3.3 Previous Block Position.

5 OVERVIEW

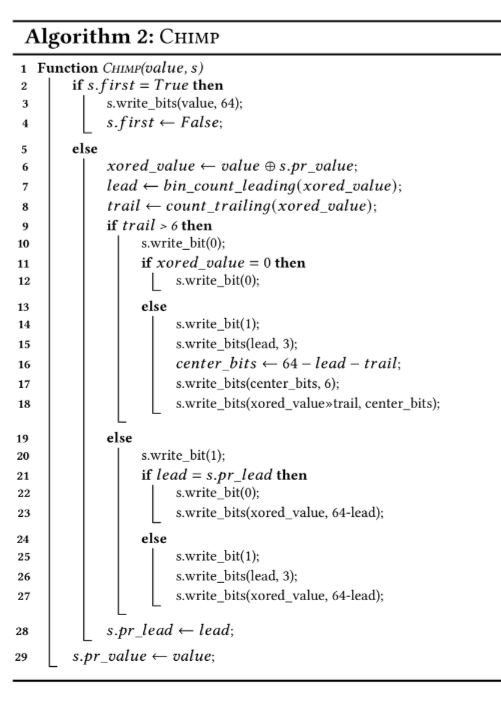
5.1 Our Chimp Algorithm

5.1.1 Possible Flag Sequences

之前的研究表明相邻数据完全相同的概率并不大，使用最少的比特位来表示最常见的情况，能够提升压缩比。

6 效果对比

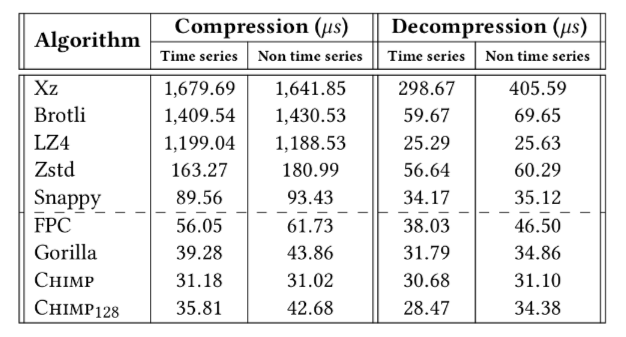
6.1 Compression size result

6.2 Compression and decompression time